Easy to understand! Explain PID

Today I will explain to you what is PID in form of pictures and texts? What is function of each PID parameter? Where will PID be used? Come learn together!

What is a PID?

The PID (proportional-integral-derivative) controller is a very common control algorithm.

PID has 107 years of history, it's not something very sacred, everyone should have seen practical use of PID.

For example, a quadrocopter, or a balancer ... and a car cruise control, a temperature controller on a 3D printer ....

Similarly, when it is necessary to "keep stable" some physical quantity (such as maintaining balance, stabilizing temperatures, speeds, etc.), PID comes in handy.

Then question is:

For example, I want to control a "heater" to keep a pot of water at 50°C. Why should I use calculus theory for such a simple task?

You must be thinking:

Isn't it so easy~ Just let it heat up when temperature is below 50 degrees, and turn off power if temperature is above 50 degrees, right? A few lines of code can be written in minutes with Arduino.

That's right~ You can actually do it when demands are low~ But! In other words, you know what problem is:

What if my control object is a car?

If you want car to stay at 50 km/h, why would you want to?

Imagine that cruise control computer determines that vehicle's speed at a certain point in time is 45 km/h. He immediately commands engine: Accelerate!

The result was that engine suddenly went to 100% full throttle and car accelerated to 60 km/h with a roar.

At this time, computer issued another command: brake!

As a result, a squeak ...... Wow ...... (Passenger spit)

Therefore, in most cases, using a "switchable value" to control a physical quantity is relatively simple and crude. Sometimes it is impossible to maintain stability. Since single-chip microcomputers and sensors are not infinitely fast, data collection and control take time.

In addition, control object has inertia. For example, if you unplug a heater from mains, its "waste heat" (i.e., thermal inertia) can raise temperature of water for some time.

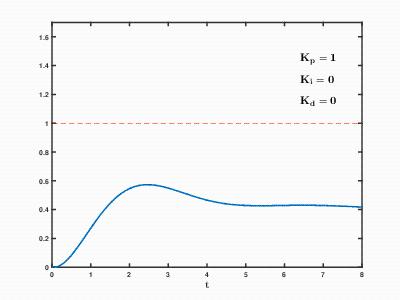
The role of three control links

Let's talk only about three most basic parameters of PID controller: kP, kI, kD.

KP Role:

P stands for proportion. It has most obvious effect and simplest principle. Let's start with this:

A value to be monitored, such as water temperature, has a current "current value" and an expected "target value".

When difference is close, let heater "slightly" warm up.

If for some reason temperature drops too much, turn on heater "a little harder".

If current temperature is much lower than set temperature, let "fire" heater warm up so that water temperature reaches set temperature as soon as possible.

This is role of P. Compared to switch control method, it is much more "soft and elegant"

While writing a program, let deviation (target value minus current) and "adjustment force" of adjustment device become linear, and simplest "proportional" control can already be implemented~

The larger kP, more aggressive regulation, and smaller kP, more conservative regulation.

If you make a self-balancing car with P function, you will find that self-balancing car "vibrates" back and forth near balancing angle and is more difficult to stabilize.

If you've made it this far, congratulations! Success is just one small step~

KD Role:

The role of D is better understood, so let's talk about D first and then I.

Only now we have role of P. It is not difficult to find that only P seems to be unable to get balancing station to stand up, and water temperature is also shaky, as if whole system is not particularly stable and is “vibrating” all time.

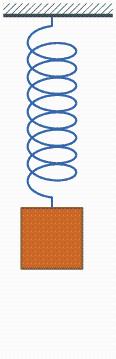
Imagine a spring: now in an equilibrium position. Give him a jerk, then let go. At this point it will vibrate. Since resistance is very small, it can fluctuate for a long time before settling again in equilibrium position.

Imagine: if system shown in picture above were immersed in water, it would also be pulled: in this case, time to return to equilibrium position would be much less.

We need a control effect so that "rate of change" of controlled physical quantity tends to 0, which is similar to "damping" effect.

Because when it is closer to target, control effect of P is relatively small. The closer to target, softer action of P. There are many internal or external factors that cause amount of control to fluctuate within a small range.

The function of D is to make velocity of a physical quantity approach 0. Whenever quantity has a velocity, D will apply force in opposite direction and try to stop change.

The larger kD parameter, greater braking force in direction opposite to speed.

If it's a balancing car, plus two control functions P and D, if parameters are adjusted correctly, it should be able to stand up ~ cheers.

Wait, there seems to be another one of three PID brothers. It seems that PD can keep physical quantity stable, so why would I need it?

Because we missed an important situation:

The role of kI:

Take hot water as an example. Suppose someone took our heater to a very cold place and started boiling water. Must be burned to 50°C.

Water temperature will slowly rise under P. When it reached 45℃, he discovered a bad thing: The weather is too cold, and water cooling rate is equal to heating rate controlled by P.

How to do it?

Brother P. thinks this: I'm already very close to goal, and I just need to warm it up a little.

Brother D thinks so: heating and cooling are equivalent, temperature does not fluctuate, and I don't seem to need to adjust anything.

As a result, water temperature always stays at 45°C, never reaching 50°C.

As humans, we know, based on common sense, that heating power should be increased. But how much to count?

The method proposed by senior scientists is truly original.

Specifies an integer. As long as deviation exists, it will continue to integrate (accumulate) deviation and reflect it in strength of adjustment.

Thus, even if difference between 45°C and 50°C is not too large, over time, until target temperature is reached, integral willshould increase. The system will gradually realize that target temperature has not yet been reached, it's time to increase power!

Once target temperature has been reached, provided that temperature does not fluctuate, integral value will no longer change. At this time, heating power is still equal to cooling power. However, temperature was stable at 50°C.

The larger value of kI, greater multiplication factor during integration, and more obvious effect of integration.

Therefore, function of I is to reduce error in a static situation and bring controlled physical quantity as close as possible to target value.

I still have a problem when I use it: I need to set integral limit. So that integral volume is not too large at beginning of heating, it is difficult to control it.

PID control principle:

1. Proportional (P) control Proportional control is simplest control method. Its controller output is proportional to error input. When there is only proportional control, a steady-state error occurs at output of system.

2. Integral (I) control In integral control, controller output is proportional to integral of error input. For an automatic control system, if a steady-state error occurs after entering a steady state, control system is called a steady-state error or simply a differential system. To eliminate steady-state error, it is necessary to introduce an “integral term” into controller. The cumulative term is time-dependent error integral, and cumulative term increases with time. Thus, even if error is small, integral term will increase with time, causing controller output to increase to further reduce steady-state error until it becomes zero. Thus, a proportional-integral (PI) controller can make sure that system does not have a steady-state error after entering a steady state.

3. Derivative (D) Control In differential control, controller output is proportional to differential of error input (that is, rate of change of error). The automatic control system may fluctuate or even become unstable during error handling tuning process.

The

The reason is that there are large inertial components (links) or lagging components that have an error suppression effect, and their changes always lag behind error changes.

The solution is to "promote" a variation of error suppression effect, that is, when error is close to zero, error suppression effect should be zero. That is, it is often not enough to enter into controller only "proportion"rational" element. The function of proportional element is only to amplify magnitude of error. Now we need to add a "differential element" that can predict trend of error.

In this way, a P+D controller can provide a control effect of suppressing an error equal to zero or even a negative value in advance, thus avoiding a severe overrun. Therefore, for a controlled object with a large inertia or delay, a proportional-derivative (PD) controller can improve dynamic characteristics of system in process of regulation.

General method for tuning PID controller parameters:

Setting parameters of PID controller is main content of design of control system. It determines size of proportional gain, integral time and derivative time of PID controller according to characteristics of controlled process. There are many methods for tuning PID controller parameters, which can be divided into two categories:

Theoretical calculation and adjustment method

It is mainly based on mathematical model of system to determine parameters of controller through theoretical calculations. The calculated data obtained by this method cannot be used directly and must be corrected and changed by engineering practice;

Technical setting method

It is mainly based on engineering experience and is carried out directly when testing control system. The method is simple and easy to learn and is widely used in engineering practice. PID parameter engineering tuning methods mainly include critical ratio method, response curve method and damping method.

These three methods have their own characteristics, and their common point is to pass test and then adjust controller parameters according to engineering experience formula. But whatever method is used to obtain parameters of controller, it must be tuned and improved in real operating conditions.

Currently, critical ratio method is commonly used. The steps for tuning PID controller parameters using this method are as follows: * First, pre-select a short enough sampling period for system to work;

Only add proportional control until input transient response is critical, at which time record proportional gain and critical period of oscillation;

The parameters of PID controller are calculated by formula at a certain degree of regulation.

PID parameter setting: rely on experience and familiarity with process, refer to measurement trackingvalue and setpoint curve to adjust size of P, I, D.

Common formulas in book:

Searching for best parameter, searching in order from smallest to largest;   先 是 积分 积分 ， 最后 把 微分加 微分加   曲线 振荡 频繁 比例 要 放大 ；   曲线 绕大湾 绕大湾 比例 比例 ， ， ， ， ， ， ， ， ，度盘 往 小 扳 ；   曲线 回复 慢 ， 积分 往 下降 ； ；   曲线 周期 长 积分 时间 加长 ；   曲线 振荡 频率 先 把 把 把 把 把 把 把 把 把 把 把 把 把 把把 把 把 把 把 微分 降 下来 ；   动差 大 来 波动。 微分 时间 加长 ；   理想 两 个 ， 后低 后低 4 比 1 ； 

Take a look at second adjustment and analyze whether quality of adjustment will not be low.

I personally believe that setting of PID controller parameters depends, on one hand, on specific conditions of control object, and, on other hand, on experience. P to decide oscillation amplitude. If P is large, oscillation amplitude will be large, but oscillation frequency is small, and system will take a long time to stabilize, I must decide action reaction speed. If I is large, response speed is low, and vice versa. ; D is used to eliminate static errors, usually D is set relatively small and has a relatively small impact on system.

How to better tune PID parameters:

(1) Proportional control settingChange proportional control function from small to large, observe each response until you get a response curve with fast response and small overshoot.

(2) Integral link settingIf steady state error cannot meet requirements of proportional control, integral control is required.

First decrease proportional gain selected in step (1) to 50-80% of original value, then set integral time to a larger value and observe response curve. Then reduce integration time, increase integral effect, adjust proportionality factor accordingly, and try again and again until a satisfactory answer is obtained, and then determine proportionality and integral parameters.

(3) Derivative settingIf, after step (2), PI control can only eliminate steady-state error, but dynamic process is not satisfactory, then it is necessary to add differential control to form PID control. Set differential time TD=0 first, increase TD gradually, and change proportional gain and integral time accordingly, and try again to obtain a satisfactory control effect and PID control parameters.

Gift Display

First watch animation to learn about PID:

The initial state of system is 0, target state is 10.

First, let's show process of bypassing the parameters.

The animation below shows respective effect of each setting:

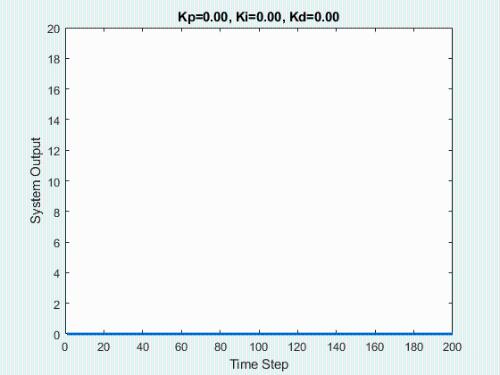
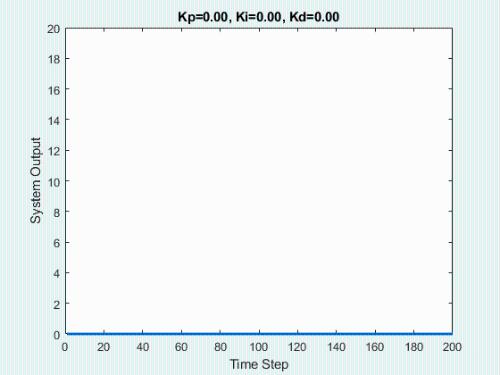
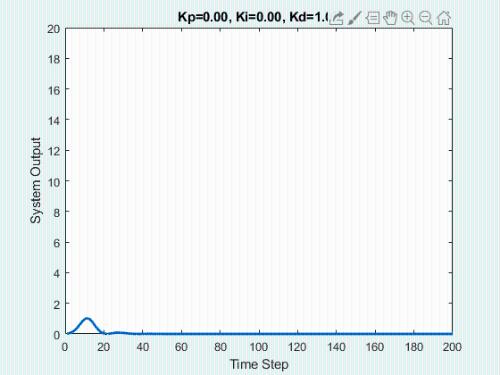
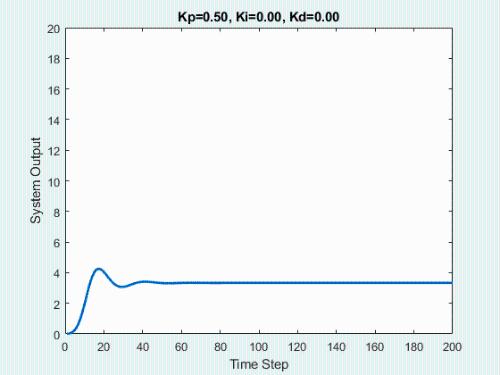
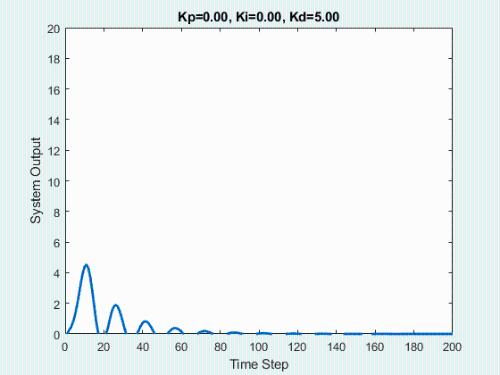
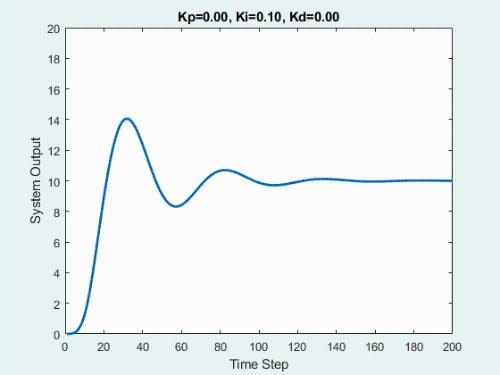
In real engineering, most widely used regulator control law is proportional, integral, differential control, called PID control, also known as PID control. PID controller has become one of core technology of industrial control due to its simple structure, good stability, reliable performance and convenient setting.

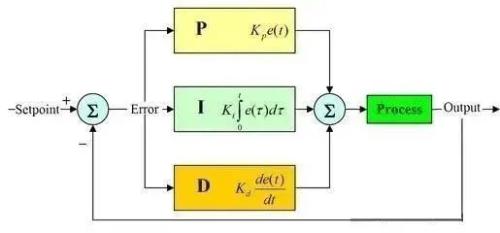
PID controller is a traditional control method that is applicable to almost all objects, such as temperature, pressure, flow, liquid level, etc. Only PID controller parameters need to be set differently in different objects. parameters are set correctly, you can achieve good results Effect. Both can reach 0.1% or even higher control requirements.

PID History

Xiao Ming was given following task: there is a leak in a tank of water (and rate of leakage is not necessarily constant), and it is required to maintain height of water surface in a certain position. water.

Xiao Ming stayed by water tank after receiving task. After a long time, he became bored, so he went to room to read novels and checked water level every 30 minutes.

Water flowed out too fast. Every time Xiao Ming came to check, almost no water came out and height was far from required height. Xiao Ming changed check every 3 minutes, and as a result, no water came out. each time it doesn’t flow much, you don’t need to add water, otherwise what comes too often is useless.

After several attempts, check every 10 minutes. This test time is called sampling period.

At first, Xiao Ming used a ladle to add water. The distance from tap to water tank was more than ten meters, and he often had to run several times to pour enough water. The speed of adding water is also faster, but tank overflowed several times and accidentally wet shoes several times. Xiao Ming used his brain again. No need to run too many times and let water overflow. The size of this water addition tool is called scale factor.

Xiao Ming also found that while water would not be added too much for overflow, it would sometimes be higher than required and there was still a danger of shoes getting wet.

He came up with another way and installed a funnel on water tank. Each time he added water, instead of pouring it directly into water tank, he poured it into funnel and let it slowly add. This solves overflow problem, but water addition rate is slow again, and sometimes it cannot catch up with water leakage rate.

So he tried changing different sizes and calibers of funnels to control rate of water addition, and finally found a funnel that satisfied him. The funnel time is called integration time.

Xiao Ming finally breathed a sigh of relief, but requirements of task suddenly became more stringent, and requirements for timeliness of water level control improved significantly, salary. Xiao Ming is in trouble again!

So he used his brain again and finally let him come up with a way. He often places a basin of spare water next to him. When he finds that water level is low, he simply pours it out,without passing through funnel. This ensures timeliness, but water level will sometimes be much higher.

He drilled a water hole just above required water surface, and then connected a pipe to a spare bucket below to allow excess water to flow out of hole above. The rate at which this water flows out is called differential time.

I've seen a few posts with questions about fetch loop, so I thought about that story for a while. The differential analogy is a bit contrived, but for understanding, hehe, an entry level is enough, if it can help beginners understand PID, that would be enough for me.

Xiao Ming's experiment in this story was done step by step independently, but actual water addition tool, funnel diameter, and overflow hole size will affect water addition rate and water level. Change results of previous experiments.

Xiao Ming's experiment in this story was done step by step independently, but actual water addition tool, funnel diameter, and overflow hole size will affect water addition rate and water level. Change results of previous experiments.

A person uses a PID control method to pour half a cup of water with a scale into a cup with a kettle, and then stops;

Setting value: half scale of a glass of water;

Actual value: actual amount of water in cup;

Output value: amount of water poured out of kettle and amount of water scooped out of cup;

Measurement: human eyes (analogue of sensors)

Run object: people

Performance: dousing with water

Anti-execution: salvation

(1) Phosphorus ratio control

When a person sees that amount of water in glass of water has not reached half mark of glass of water, he pours water from kettle into glass of water according to a certain amount of water, or if amount of water in glass of water exceeds scale, he scoops water from a glass of water with a certain amount of water. A single movement can stop a drink when it is less than half a glass or half a glass is too much.

Explanation: P-proportional control is simplest control method. Its controller output is proportional to error input. When there is only proportional control, a steady error (Steady Error) occurs at output of system.

(2) PI integral control

Pour a certain amount of water into a cup of water. If you find that amount of water in cup is not marked, keep pouring it. Later, when you find that amount of water is more than half a glass, you will scoop water from cup, and then refill water if there is not enough, simply scooping water until water volume reaches mark.

AnnounceDescription: In integral I-control, output of controller is proportional to integral of error input signal. For an automatic control system, if a steady-state error occurs after entering a steady state, control system is said to have a steady-state error or simply a System with Steady-state Error.

In order to resolve a persistent error, an "integral term" must be entered into controller. The cumulative term is time-dependent error integral, and cumulative term increases with time. Thus, even if error is small, integral term will increase with time, causing controller output to increase to further reduce steady-state error until it becomes zero.

Therefore, a proportional-integral (PI) controller can make sure that system does not have a steady-state error after entering a steady state.

(3) Differential PID controller

This means that people's eyes look at distance between volume of water in cup and scale. When gap is large, use a large water bottle to pour water. When people see that volume of water is approaching scale, reduce volume of kettle The amount of water slowly approaching scale until it remains in cup.

If it can stop exactly at scale position, there is no static difference control; if it stops near scale, it has static difference control.

Explanation: With differential control D, output of controller is proportional to differential of error input signal (that is, rate of change of error).

In engineering practice, most widely used regulator control law is proportional, integral, differential control law, referred to as PID control, also known as PID control.

It has been almost 70 years since advent of PID controller, which has become one of mainstream industrial control technologies due to its simple structure, good stability, reliable performance and convenient setting.

When structure and parameters of controlled object cannot be fully understood or an accurate mathematical model cannot be obtained, and other methods of control theory are difficult to accept, structure and parameters of system controller must be determined empirically. and on-site debugging. At present, it is most convenient to apply PID control technology.

That is, when we do not fully understand system and controlled object, or cannot obtain system parameters through effective measurement methods, it is most appropriate to use PID control technology. PID control, in practice there are also PI and PD control.

The PID controller is based on system error, using proportional, integral and derivative to calculate control amount dfor control.

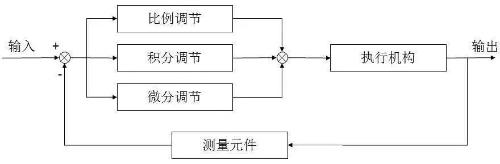
PID parameters

1. Proportional (P) control

Proportional control is simplest method of control. Its controller output is proportional to error input. When there is only proportional control, a steady error (Steady Error) occurs at output of system.

2. Integral (I) control

In integral control, controller output is proportional to integral of error input. For an automatic control system, if a steady-state error occurs after entering a steady state, control system is said to have a steady-state error or simply a System with Steady-state Error. To eliminate steady-state error, it is necessary to introduce an “integral term” into controller. The cumulative term is time-dependent error integral, and cumulative term increases with time. Thus, even if error is small, integral term will increase with time, causing controller output to increase to further reduce steady-state error until it becomes zero. Thus, a proportional-integral (PI) controller can make sure that system does not have a steady-state error after entering a steady state.

3. Derivative (D) control

In differential control, output of controller is proportional to differential of error input (that is, rate of change of error). The automatic control system may fluctuate or even become unstable during error handling tuning process.

The reason is that due to presence of large inertial components (couplings) or lag (retarded) components, which have effect of suppressing errors, their changes always lag behind changes in errors. The solution is to make error suppression effect change "advanced", that is, when error is close to zero, error suppression effect should be zero.

That is, it is often not enough to enter only a "proportional" element into controller. The function of proportional element is only to amplify magnitude of error. Now it is necessary to add a "differential element", which can predict change in error. In this way, proportional + differential controller can make error suppression control effect to be zero or even a negative value in advance, thus avoiding adjustable amount being seriously exceeded. Therefore, for controlled object with large inertia or lag, proportional-derivative (PD) controller can improve dynamic performance of system in process of regulation.

When tuning PID parameters, if there is a theoretical method for determining pairsPID parameters, this is of course most ideal method, but in practical applications more PID parameters are determined by trial and error.

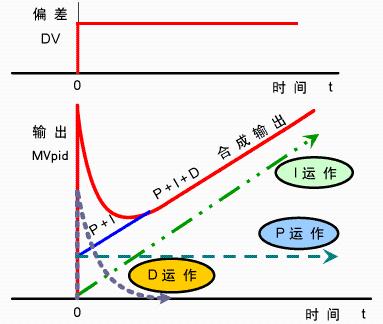
Increasing proportional gain P tends to speed up response of system, and it is beneficial to reduce static error when there is a static error, but too large a proportional gain will result in system having a relatively large overshoot. and cause fluctuations, resulting in poor stability.

Increasing integration time I is useful for reducing overshoot, reducing oscillation, and improving system stability, but system static error recovery time is increased.

Increasing differential time D is useful for increasing system response speed, reducing system overshoot, and improving stability, but system's ability to suppress interference is weakened.

When running test, you can refer to influence trend of above parameters on system control process, and follow steps of setting proportion, then integral, and then differential to adjust parameters.

PID parameter setting methods

Setting parameters of PID controller is main content of design of control system. It determines size of proportional gain, integral time and derivative time of PID controller according to characteristics of controlled process. There are many methods for tuning PID controller parameters, which can be divided into two categories:

1. Theoretical calculation and tuning method

It is mainly based on mathematical model of system to determine parameters of controller through theoretical calculations. The calculated data obtained by this method cannot be used directly and must be corrected and changed by engineering practice;

Second, technical setting method

It is mainly based on engineering experience and is carried out directly when testing control system. The method is simple and easy to learn and is widely used in engineering practice. PID parameter engineering tuning methods mainly include critical ratio method, response curve method and damping method. The three methods have their own characteristics, and their common point is to pass test and then adjust controller parameters according to engineering experience formula. But whatever method is used to obtain parameters of controller, it must be tuned and improved in real operating conditions.

Currently, critical ratio method is commonly used, and steps for tuning PID controller parameters using this method are as follows:

First, preselect a sampling period that is short enough for system to work;

Add proportional control only until system experiences a critical swing in transient response to input, and inthis time, write down proportional gain and critical period of oscillation;

The parameters of PID controller are calculated by formula at a certain degree of regulation.

PID parameter setting: Rely on experience and familiarity with process, refer to measured value tracking and set value curve to adjust P, I, D size.

Common formulas:

Find best parameter setting, search in order from smallest to largest;

First proportion, then integral, and finally differential;

The curve fluctuates frequently and scale scale needs to be increased;

The curve floats around a large bay, and scale is turned towards a small one;

The curve slowly deviates and slowly returns, and integration time decreases;

The oscillation period of curve is long and integration time should be longer:

Step 1. Set up proportional control

Change proportional control effect from small to large and watch each response until you get a response curve with a fast response and little overshoot.

Second Step: Installing Integration Link

If steady state error cannot satisfy requirements of proportional control, integral control is required. First reduce proportional gain selected in previous steps to 50-80% of original value, then set integration time to a larger value and observe response curve. Then reduce integration time, increase integral effect, adjust proportionality factor accordingly, and try again and again until a satisfactory answer is obtained, and then determine proportionality and integral parameters.

Third step: setting up a differential link

If, after above steps, PI control can only eliminate steady-state errors, but dynamic process is not satisfactory, then differential control should be added to form PID control. Set differential time TD=0 first, increase TD gradually, and change proportional gain and integral time accordingly, and try again to obtain a satisfactory control effect and PID control parameters.

15 Basic PID Concepts

If you don't have diamonds, you won't be able to work with porcelain. In order to be able to master and use PID, it is very necessary for us to learn basic concepts to arm ourselves. Some concepts will be mapped to commonly used representation methods in real design, starting with "actual:".

1. The Adjusted Quantity reflects actual amount of fluctuation of adjusted object. Adjustedthe number is constantly changing.

Real: Typically used to indicate a detected feedback value, such as yout(t).

2. Tuning Value The tuning value of a PID controller is value that people expect from adjusted value. The setpoint can be fixed or variable.

Real: artificially defined and usually denoted rin(t).

3. Control output After PID controller calculates according to change in adjusted value, it sends a command to make external execution structure act according to its requirements, that is, output of entire controller. Note difference with yout(t) custom variable, these are two completely different concepts and people often confuse two.

Fact: u(t) often occurs in formula "u(t)=kp[e(t)+1/TI∫e(t)dt+TD*de(t)/dt]".

4. Deviation entry Difference between corrected value and setpoint when entering deviation.

Real: error(t)=rin(t)-yout(t).

5. P (proportion) P is proportional effect, in other words, it is input deviation multiplied by a factor.

Fact. For example, kp and KP are same.

6. I (integral)I is an integral, in other words, it is designed to integrate input deviation.

7. D (integral) D is differential, in other words, it performs a differential operation on input variance.

8. The basic formula of PID controller The process of tuning PID controller parameters is generally that system is first adjusted to a purely proportional action, and proportional action is gradually increased so that system oscillates with a constant amplitude. , and proportional action and swing are written in a period, then proportional action is multiplied by 0.6, and integral action is expanded accordingly

KP= 0.6*KmKD= KP*π/4ω or KD= KP*tu/8KI= KP*ω/π or KI= 2KP/ tuKP: proportional control parameters;KD: integral control parameters;KI: differential control parameters;

Km: proportional value when system starts to oscillate, commonly referred to as critical proportional value;

ω: constant amplitude oscillation frequency, tu - oscillation period. Here tuω = 2π, not tuω = 1. Students of Fourier and Laplace transforms should understand why this is so, and we will not discuss it in detail here.

9. Single loop A single loop is a control system with only one PID controller.

10. Cascaded One PID controller is not enough. A cascade connection consists of connecting two PID controllers in series to form a cascadedth control system, which is also called a two-loop control system. In a cascade control system, PID controller can be divided into a main tuner and an auxiliary tuner.

Cascade controlIn system, PID controller which is to control controlled value is called main setting, and PID controller whose output directly controls action of actuator is called sub-tuning, and control output of main setting is included in sub-tuning. Tune as set sub-melody value. The main tuning uses a single-loop PID controller, and secondary tuning uses an external setpoint controller.

11. Positive effect

For a PID controller, effect that control output increases with an increase in controlled variable and decreases with a decrease in controlled variable is called PID positive action.

12. Negative consequences

For a PID controller, effect that control output decreases as controlled variable increases and increases as controlled variable decreases, is called PID negative effect.

13. Dynamic deflection

During correction process, deviation between corrected quantity and setpoint changes at any time, and deviation between them at any time is called dynamic deviation.

14. Static deflection

After correction becomes stable, there is still a deviation between corrected quantity and set value, which is a static deviation. The elimination of static deviation is achieved through integral action of PID controller.

15. Callback

The slider adjustment function is displayed so that adjusted amount starts to change from rising to falling or from falling to rising to become a callback.